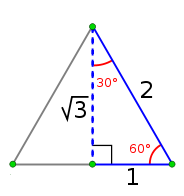
1,7320508075688774

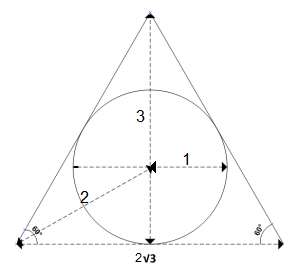
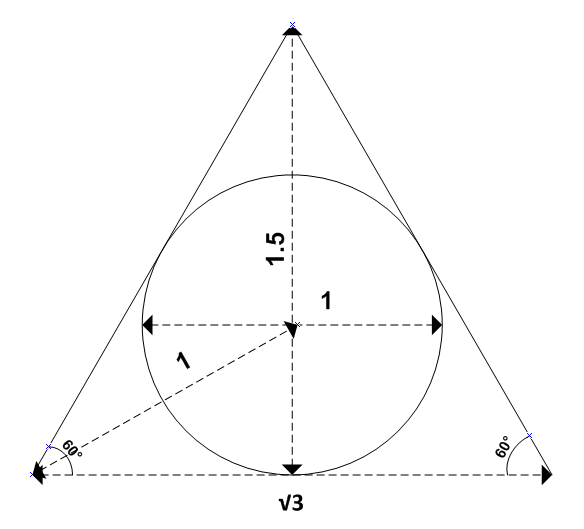
Si on encadre un cercle de diamètre 1 avec un triangle équilatéral, chaque côté du triangle est égal à racine carrée de 3. Et donc chaque carré à une aire de 3 :
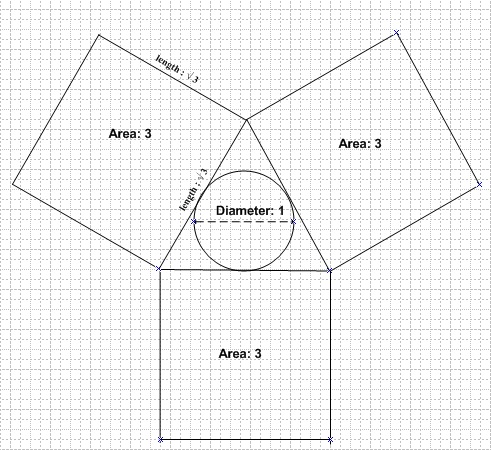
L’aire du triangle équilatéral est ( coté ² x racine de 3 ) / 4. Donc dans ce cas : ( 3 x racine de 3) /4 = 1,2990381…
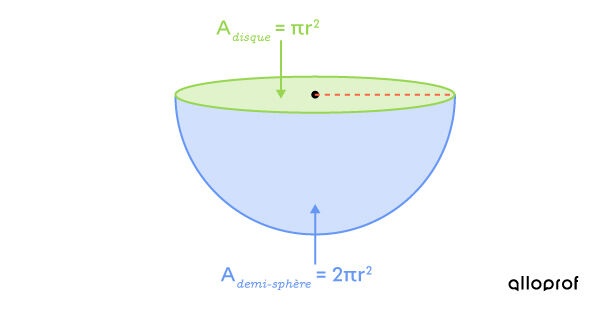
L’aire d’une sphère est égale à 4 fois l’aire du disque de même diamètre :

ou on peut dire aussi que l’aire d’une demi-sphère est égale à 2 fois l’aire du disque :
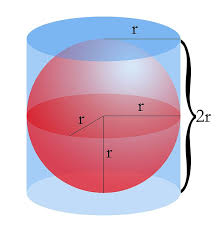
Les Surfaces (aires) de la sphère et du cylindre qui l’entoure sont égales tranche à tranche (en bleu plus clair sur les schémas ci-dessous) :
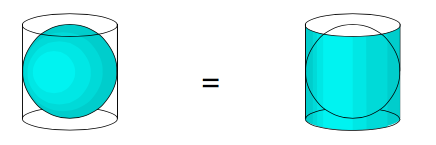
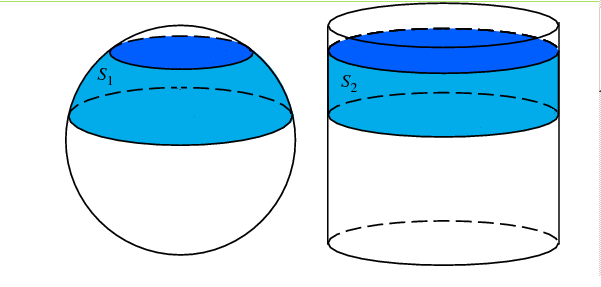

L’aire du cylindre est un rectangle refermé sur lui-même.
Proportions entre un cône, une sphère, un cylindre
Si on part d’un cercle de diamètre 1 :
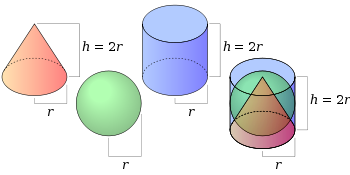
Le volume du cône de diamètre 1 et de hauteur 1 est égal à : (π×(0.5)2×1) / 3 =0.26
Le volume de la sphère de diamètre 1 est égal à : (4×π×0.53) / 3=0.52, soit deux fois le volume du cône
Le volume du cylindre est égal à : π × 0,52 × 1 = 0,7854, soit une fois et demi le volume de la sphère, ou 3 fois le volume du cône.
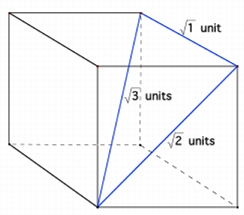
On retrouve la racine de 3 dans la géométrie du cube. Si on a un cube avec un côté de 1, alors la diagonale du cube est racine de 3 :
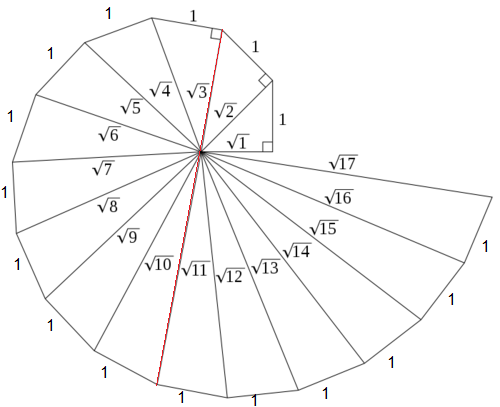
Si on considère un triangle équilatéral de 1 de côté, son aire est de (racine de 3) / 4:
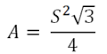
Et l’aire du cercle circonscrit est de (racine de 3) / 3
Et l’aire du disque inscrit est de (racine de 3) / 6
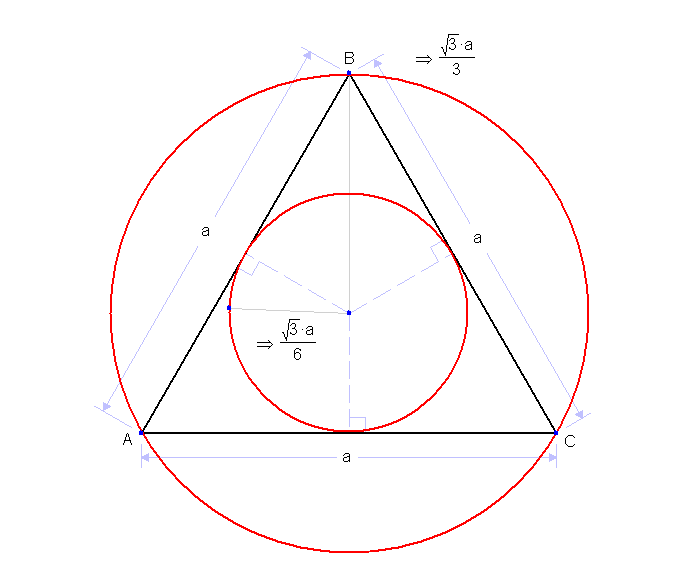
On peut alors se demander à quoi correspondrait l’aire (racine de 3) / 5 , dont la valeur est 0,34641016
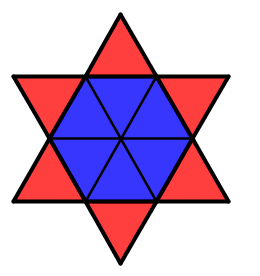
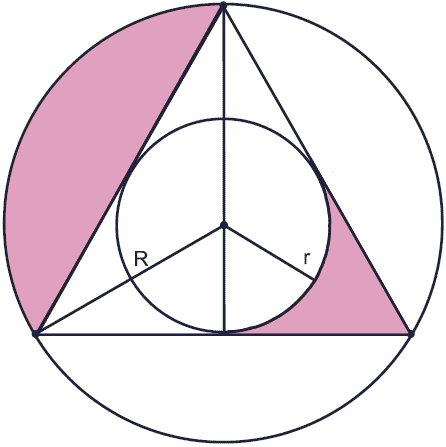
Dans cette figure intéressante, on peut aussi noter que l’aire de la zone rose est égale à 3 fois l’aire de la zone jaune :
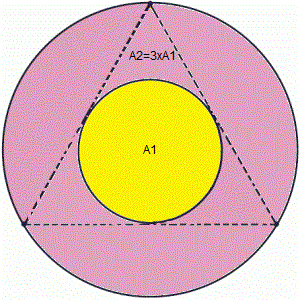
Et donc l’aire de chacun des sous-ensembles roses est égale à l’aire du disque jaune :
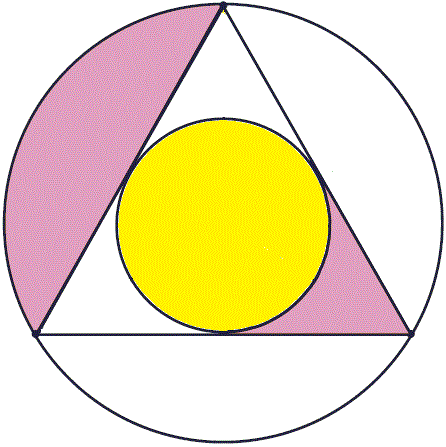
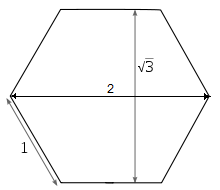
Et la racine de 3 dans un hexagone. Si la largeur de l’hexagone est 2, alors sa hauteur est racine de 3 :
Et dans l’aire d’un triangle équilatéral. Si le côté fait 1, alors l’aire est égale à (racine carrée de 3) / 4 :
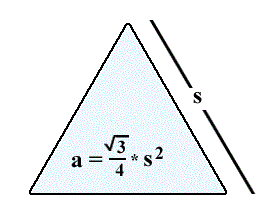
Et si le côté fait 2, alors la hauteur du triangle est racine carrée de 3 :